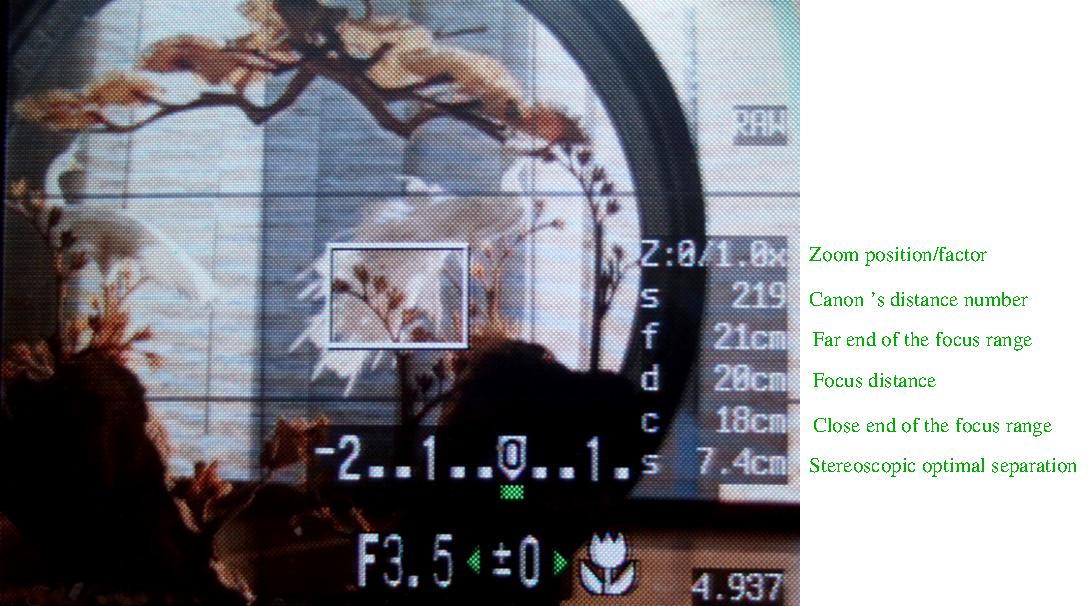
I give here a brief summary of work I have done to display the subject distance and the ratio of the subject distance to the hyperfocal distance on the LCD display of my A620.

There are two problems I wished to address. The first problem is that there is no clear indication of where 'Infinity' is and where the hyperfocal distance is on the distance scale when in manual focus mode on the A620. The second problem is that the number returned by Canon as the distance number (s) is off the mark starting at distances half the hyperfocal distance.
Thanks to the 'chdk' software by Vitaly and GrAnd and possibly others, I was able to explore the relation between the actual subject distance and the Canon distance number.
The methodology I used was to set the camera at a measured distance from a contrasty and well lit target and then activate the autofocus system to get the Canon distance number. I could not do it the other way around by manually focusing on the target because of the limited resolution of the LCD display and the imprecise control provided by the camera keyboard.
Following that method I collected nearly 500 samples of (distance, Canon number, zoom number).
The first model I used was to manually draw a curve averaging the data in log-log coordinates. Working with that model was a source of insights that led me to look for an internal model that could explain some of the data.
The second model I used was based on a simple theory of the lens focusing mechanism. I assume the following relation between the movement of the lens 'x' and the Canon distance number 's'.
(1) x = a0 + a1/s
where 'a0' and 'a1' are model constants. I use the thin lens model (elementary optics here).
(2) D = f + f^2/x
D: "Distance between the subject and the thin lens"
f: "Focal length of the lens: 7.3mm up to 29.2mm"
x: "Distance between the thin lens and the image of the subject minus 'f'"
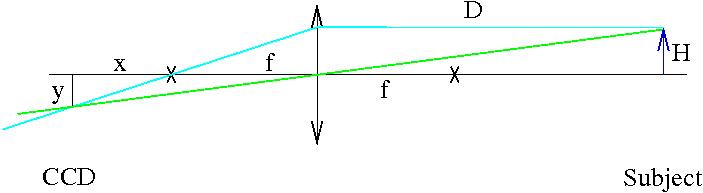
The relation between the thin lens model used here and the A620 lens is illustrated by the following diagram.
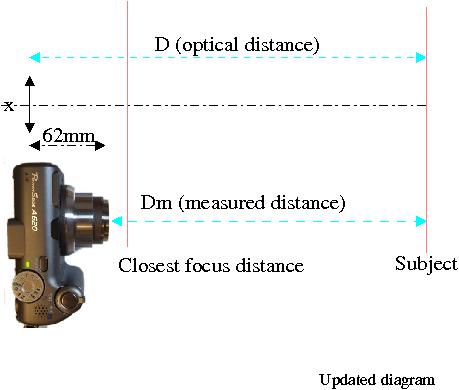
(Dm) D = Dm - d0 [definition]
'Dm' denotes the value returned by the distance measuring procedure I used; namely the distance between the subject and the rim of the lens without zoom (f=7.3mm). 'd0' is a model constant that needs to be estimated as part of the calibration. 'd0' turns out to be a negative number.
Please note that there is an error in the plot diagrams. 'Dm' should be substituted for 'D' in the titles and the formulas that appear in the plot diagrams.
Plots of 'x' versus 'Dm' support the hypothesis (equation 1) that is the basis of this model.
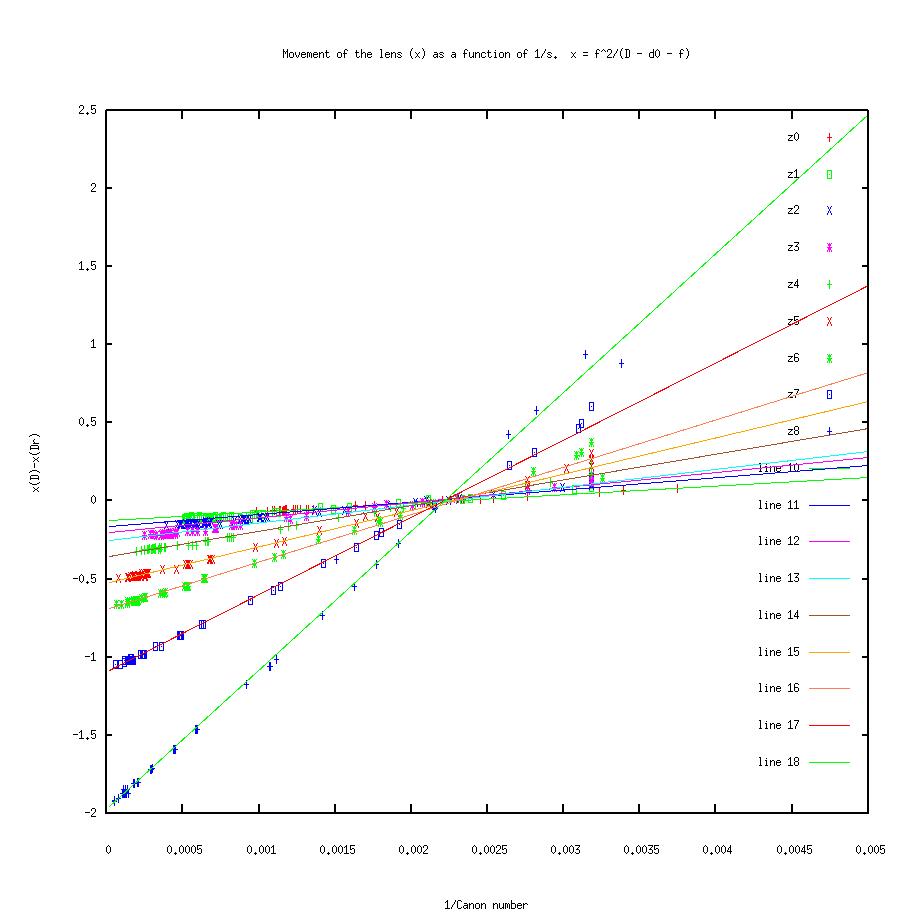
Combining equations (1), (2), and (Dm) I get the following relation between measured distance 'Dm' and 's'.
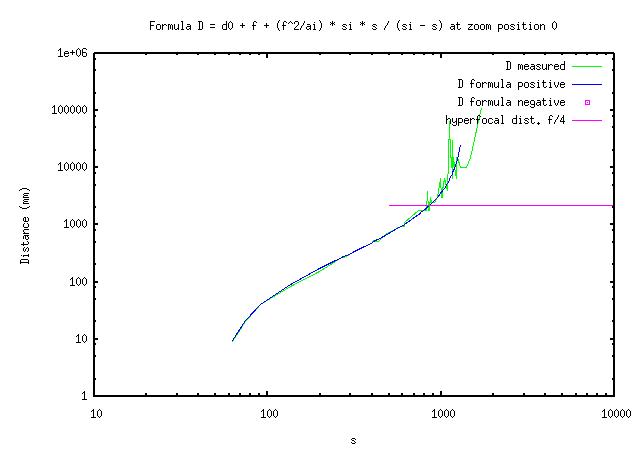
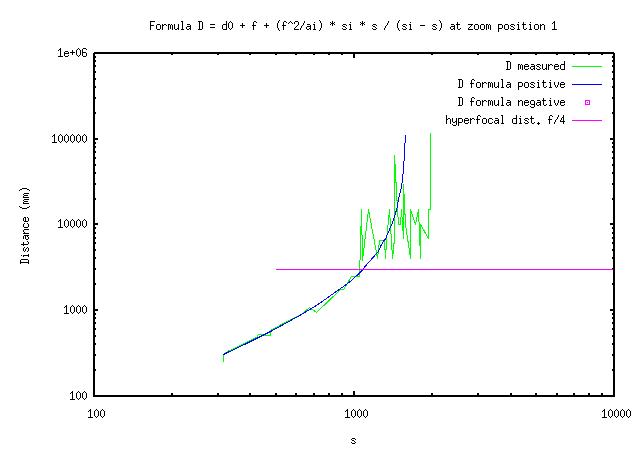
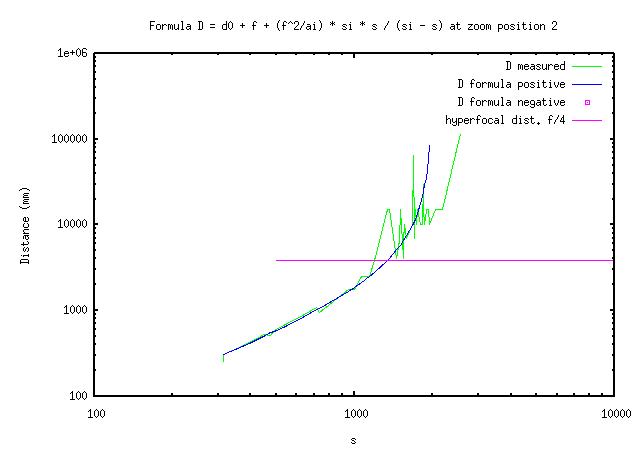
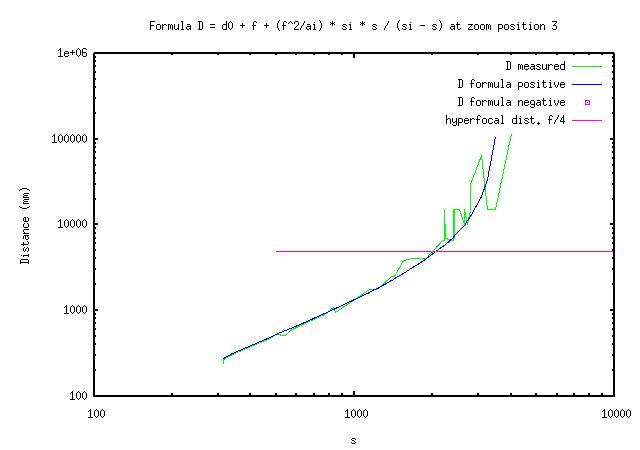
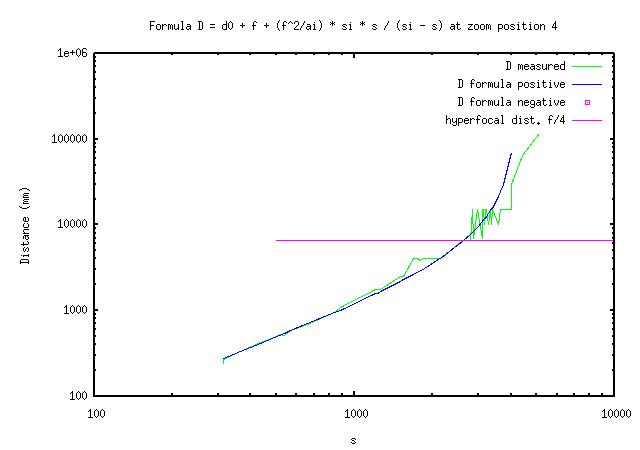
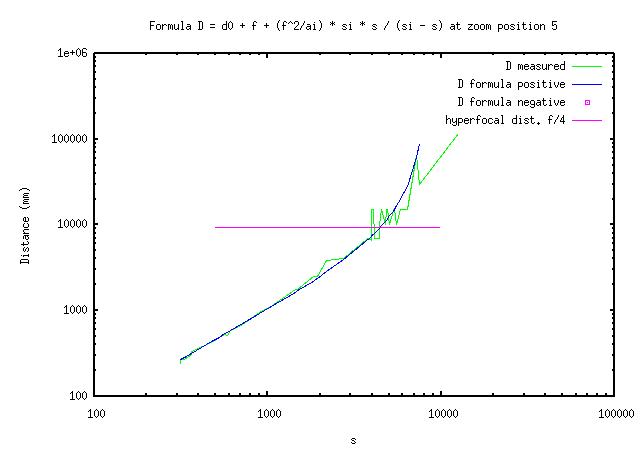
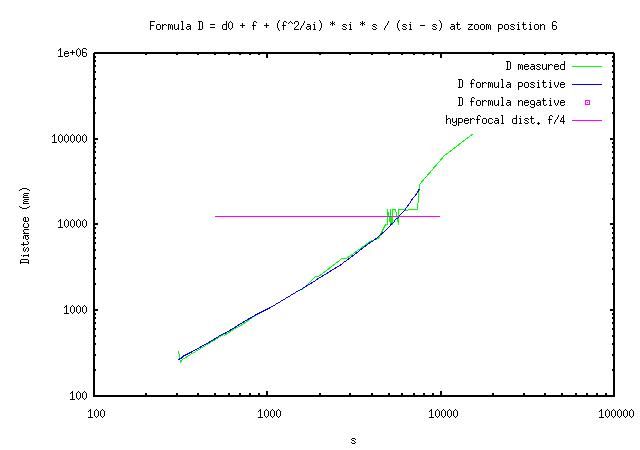
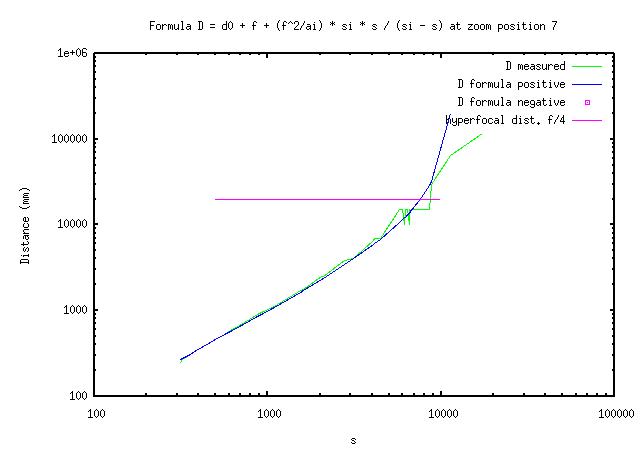
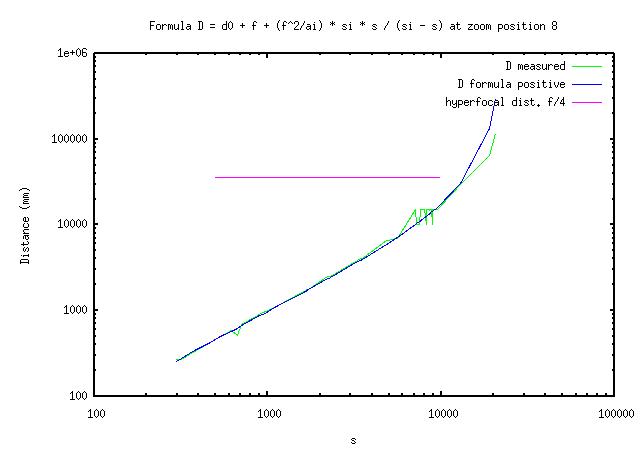
(3) Dm = d0 + f + (f^2/a1) * si * s / (si - s) [1,2,Dm]
where 'si' denotes the value of 's' for a far away subject (infinity). The corresponding value of 'x' is then 0.
In the case of my A620 the ratio f^2/a1 is close to 1 which makes me conjecture that the actual focal length is slightly different than the nominal focal lengths listed in array 'f' below.
The tree parameters I adjust are 'd0', 'a1' and 'si'. I adjust the parameters manually by trial and error using a program to plot graphs of equation (3) in log-log coordinates on top of my data. Here are the results.
float f_a[] = {7.300,8.460,9.565,10.835,12.565,14.926,17.342,21.709,29.200};
float d0[] = {-61.7, -61.7, -61.7, -86.4, -61.7, -61.7, -61.7, -61.7, -61.7};
float a1[] = {55.2, 77.8, 96, 114, 165, 233, 303, 495, 888};
float si[] = {1350, 1590, 1984, 3614, 4248, 8104, 10341, 11903, 21930};
I computed the standard deviation of '1/s' for values of 's' for which I had enough data points. I get numbers ranging from 50e-6 at 7.3mm focal length to 10e-6 at 29mm. Then I computed the sensitivity of the calculated distance to those fluctuations in '1/s'.
D = f + (f^2/a1)/((1/s) - (1/si)) [1,2] dD/d(1/s) = -(f^2/a1)/((1/s) - (1/si))^2 (dD/D)/d(1/s) ~ -/((1/s) - (1/si))
I wish to compare the fluctuation in distance 'dD' to the depth of field. Given the hyperfocal distance (H), the half depth of field (DOF2) at distance 'D' is larger than 'D^2/H'
H = f + f^2/(fn*coc)
DOF2 > D^2/H
with fn f number (2.8, 4, 5.6, 8, ...)
coc Circle of confusion (typically 6e-3mm)
So,
dD/DOF2 < (dD/D) * (D/DOF2)
< f^2/(fn * coc) * d(1/s)/(f^2/a1)
Taking 'd(1/s)' as the standard deviation of '1/s' for some given values of 's' at all focal lengths, I find that in the cases where I have enough measurements, the distance returned by the autofocus fluctuates between 15 and 35% of the half depth of field within one standard deviation.
I programmed formula (3) on my A620 using the 'chdk' and I added two lines to the OSD/MISC window
Dm as computed by the formula (3), and Dm/H the ratio between the distance and the hyperfocal distance.
The good thing is that the formula works as expected at distances smaller than H/2 on my A620.
The not so good is that the distance number tends to jump rather than to increase smoothly as I move away from the subject from as close as 1m at 7.3mm focal length (1.2m ... 1.7m, 1.9m, 2.1m ...).
The bad news is that the distance number both jumps and may be off the mark when getting to the hyperfocal distance. On top of that, I find that when I turn the camera off and back on some times later, the distance numbers may be different.
I enjoy a nice distance display on my A620.
The big question now is whether the calibration numbers I use for my A620 work for other A620's.
Richard Lemieux. Specification: Distance computations for my Powershot A620.
rf_3.c This is the latest edition of the program.
Here is an example of a situation where focusing using the program rf_3.c is helpful. In Av mode, select f/8 and manual focus mode. Adjust the distance to set the far distance number (f) either to Inf or to a large negative number. Make a note of the close distance number (c) (37 cm in this case). Finally position the camera at 37 cm from the close subject (the leaf here). I use the autofocus to get to this point and then select manual focus to set the (c) number back (to 37 cm here).
